nicht angemeldet
Mathematik zur Wochenmitte
Gunnar Bittersmann
Mathematik zur Wochenmitte
Gunnar Bittersmann
Tabellenkalk
MudGuard
Rolf B
Matthias Apsel
Die rote Linie der Länge 2 steht senkrecht auf den Basen der drei Halbkreise. Wie groß ist die gelb schraffierte Fläche?
(Aufgabe gefunden bei Catriona Shearer)
LLAP 🖖
--
„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“ —Kurt Weidemann
„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“ —Kurt Weidemann
-
-
@@Tabellenkalk
Ich seh keine gelbe Schraffur!?
Ich könnte jetzt photoshoppen …
Ach was! s/schraffierte/ausgemalte
LLAP 🖖
--
„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“ —Kurt Weidemann-
Hallo,
Ach was! s/schraffierte/ausgemalte
Ah, guck und plötzlich kann ich das Gelb sehen!
Gruß
Kalk
-
-
Hi,
Wie groß ist die gelb schraffierte Fläche?
Ich seh die deutlich!
Sind halt unendlich viele Schraffurlinien, so daß die Lücken dazwischen nicht mehr sichtbar sind …
cu,
Andreas a/k/a MudGuard-
@@MudGuard
Sind halt unendlich viele Schraffurlinien, so daß die Lücken dazwischen nicht mehr sichtbar sind …
So viele sind’s gar nicht. Es ist ein JPEG – so komprimiert, dass die Linien verschwimmen.
LLAP 🖖
--
„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“ —Kurt Weidemann-
Hi,
Es ist ein JPEG
warum? Dafür wäre doch svg viel besser geeignet 😉
cu,
Andreas a/k/a MudGuard
-
-
-
-
Hi,
Die rote Linie der Länge 2 steht senkrecht auf den Basen der drei Halbkreise. Wie groß ist die gelb schraffierte Fläche?
Täusche ich mich, oder ist die Aufgabe so nicht lösbar?
Ich glaube, daß eine einzige Längenangabe nicht ausreicht.cu,
Andreas a/k/a MudGuard-
Hallo,
Hi,
Täusche ich mich, oder ist die Aufgabe so nicht lösbar?
Ich glaube, daß eine einzige Längenangabe nicht ausreicht.Ich hab die Figur schon mal gesehen und fürchte, es gibt da eine verborgene Gesetznäßigkeit, die dafür sorgt, dass die eine Angabe ausreicht…
Gruß
Kalk -
@@MudGuard
Täusche ich mich, oder ist die Aufgabe so nicht lösbar?
Ich glaube, daß eine einzige Längenangabe nicht ausreicht.Protip: Wenn dir eine Längenangabe fehlt, dann nimm die als Parameter. Wer weiß, vielleicht fällt der am Ende der Berechnung ja wieder raus …
LLAP 🖖
--
„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“ —Kurt Weidemann -
Hallo MudGuard,
du täuschst Dich.
Rolf
--
sumpsi - posui - clusi-
Hi,
du täuschst Dich.
Ja, scheint so. Jetzt krieg ich tatsächlich ein Ergebnis.
Waren heute vormittag wohl noch Narkose-Nachwirkungen (wurde gestern operiert).
cu,
Andreas a/k/a MudGuard
-
-
-
Ich brauche den Thaleskreis-Satz richtig? Dann komme ich auf eine sehr schöne Lösung. Danke für die Aufgabe, ich liebe so was. :)
-
@@Susanne
Ich brauche den Thaleskreis-Satz richtig? Dann komme ich auf eine sehr schöne Lösung.
Ich habe ihn nicht gebraucht. Dafür war meine Lösung aber auch nicht so schön.
@ottogal und @Matthias Apsel haben mir eine sehr schöne Lösung zukommen lassen – Thales kam darin vor, ja.
LLAP 🖖
--
„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“ —Kurt Weidemann-
Hallo Gunnar,
ich habe ihn auch nicht benutzt. Wenn ich mal ein paar Thales-artige Striche hinzufüge, finde ich ähnliche Dreiecke und bestimmte Verhältnisse, die mir aus meiner Lösung bekannt vorkommen.
Allerdings musste ich für meine Lösung in die Formelsammlung für Kreissegmente schauen. Da Du mich nicht erwähnt hast, folgt wohl, dass das meine Lösung als unschön qualifziert hat.
Rolf
--
sumpsi - posui - clusi
-
-
-
@@Gunnar Bittersmann
Wie groß ist die gelb schraffierte Fläche?
Man kann – so wie ich – eine Weile rumrechnen und im zweiten Anlauf dann auf π kommen.
Oder man macht’s elegant wie @Matthias Apsel und @ottogal:
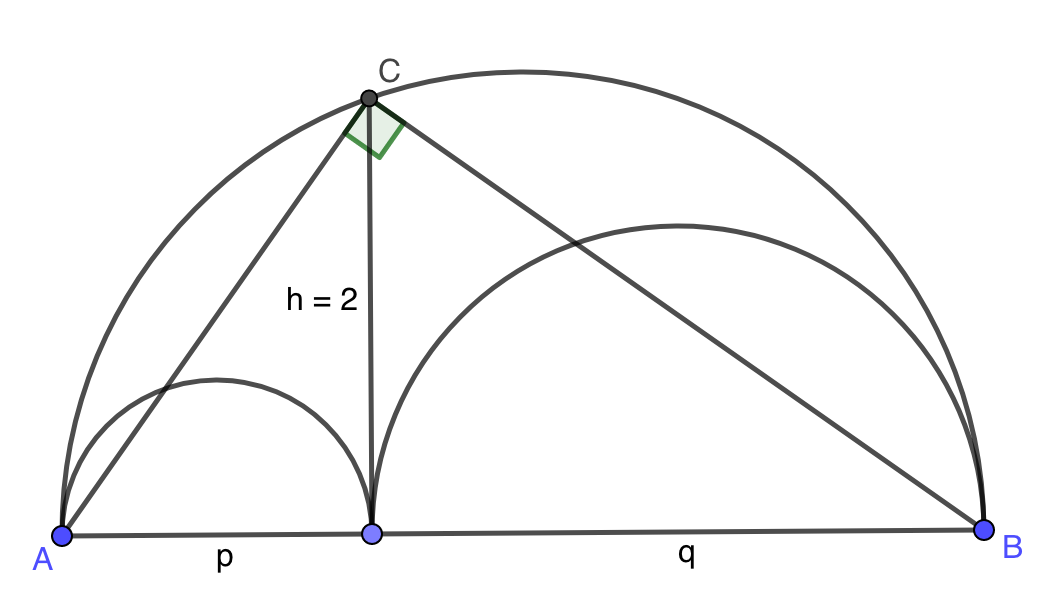
p und q sind die Durchmesser der kleinen Halbkreise; der des großen Halbkreises ist dann p + q. Dreieck ABC ist rechtwinklig (Thales), also gilt pq = h² = 4 (Höhensatz).
Die gesuchte Fläche ist: ½ (¼π (p + q)² − ¼π p² − ¼π q²) = ⅛π (p² + 2pq + q² − p² − q²) = ¼π pq = π
LLAP 🖖
--
„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“ —Kurt Weidemann-
Hallo Gunnar Bittersmann,
Oder man macht’s elegant wie @Matthias Apsel und @Orlok:
In einer PM schriebst du, @ottogal wärs gewesen.
In einer PM schrieb ich, dass du p und q vertauscht hättest: Bei Standardbezeichnung des Dreiecks ABC mit den Katheten a und b gehört der Hypotenusenabschnitt p zu a und entsprechend q zu b.
Entsprechend lauten die Kathetensätze _a_² = p_⋅_c und _b_² = q_⋅_c.
Bis demnächst
Matthias--
Pantoffeltierchen haben keine Hobbys.-
@@Matthias Apsel
In einer PM schriebst du, @ottogal wärs gewesen.
War’s auch. Sorry für die Verwechslung.
Man sollte aus einem aufpoppenden Menü nicht den erstbesten Eintrag auswählen. Das kann böse enden. ✈️⛰💥
Dieses “caused by navigational errors by the flight crew” (zu deutsch: „menschliches Versagen“) ist wohl eine gängige Umschreibung von UI-Design-Fehlern, die Bedienfehler provozieren. Und am Ende sind die Nutzer (in dem Fall: die Piloten) schuld, nicht etwa die Designer.
Glücklicherweise ist das bei der Webentwicklung ja ganz anders. Oh, wait!
In einer PM schrieb ich, dass du p und q vertauscht hättest: Bei Standardbezeichnung des Dreiecks ABC mit den Katheten a und b gehört der Hypotenusenabschnitt p zu a und entsprechend q zu b.
Ich hatte A un B vertauscht. 😜 Sorry für die Verwechslung.
LLAP 🖖
--
„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“ —Kurt Weidemann-
Hallo Gunnar Bittersmann,
Man sollte aus einem aufpoppenden Menü nicht den erstbesten Eintrag auswählen. Das kann böse enden. ✈️⛰💥
Dieses “caused by navigational errors by the flight crew” (zu deutsch: „menschliches Versagen“) ist wohl eine gängige Umschreibung von UI-Design-Fehlern, die Bedienfehler provozieren. Und am Ende sind die Nutzer (in dem Fall: die Piloten) schuld, nicht etwa die Designer.
Glücklicherweise ist das bei der Webentwicklung ja ganz anders. Oh, wait!
Dein Vorschlag zur Verbesserung der Auswahl lautet?
Bis demnächst
Matthias--
Pantoffeltierchen haben keine Hobbys.-
@@Matthias Apsel
Dein Vorschlag zur Verbesserung der Auswahl lautet?
So wollte ich mich gar nicht verstanden wissen. Hier lag tatsächlich eine Verwechslung meinerseits vor.
Aber wo wir schon mal dabei sind: Nervig finde ich, dass bei Angabe einer Sprache mittels
{:@en}das Menü aufpoppt. Nein, ich will nicht [@encoder](/users/2647) auswählen!Ich hatte seinerzeit
@enals Kurzform ins Spiel gebracht (in Anlehnung an die N3-Notation von RDF) – außerachtlassend, dass das@schon für die@-mentions verwendet wird. (Oder gab’s die zu dem Zeitpunkt noch gar nicht?)Anderes Zeichen für die Kurzform einführen? Oder kommt man aus der Nummer jetzt nicht mehr raus?
Kriegt man das kontext-sensitiv hin? Dass das Menü bei
@nur dann aufpoppt, wenn dem@nicht{:vorangegangen ist? @Christian KruseLLAP 🖖
--
„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“ —Kurt Weidemann
-
-
-
-