Informatik zum Jahresanfang – Auflösung für 9

[Gunnar Bittersmann]

@@Gunnar Bittersmann

Und wenn man den hat …

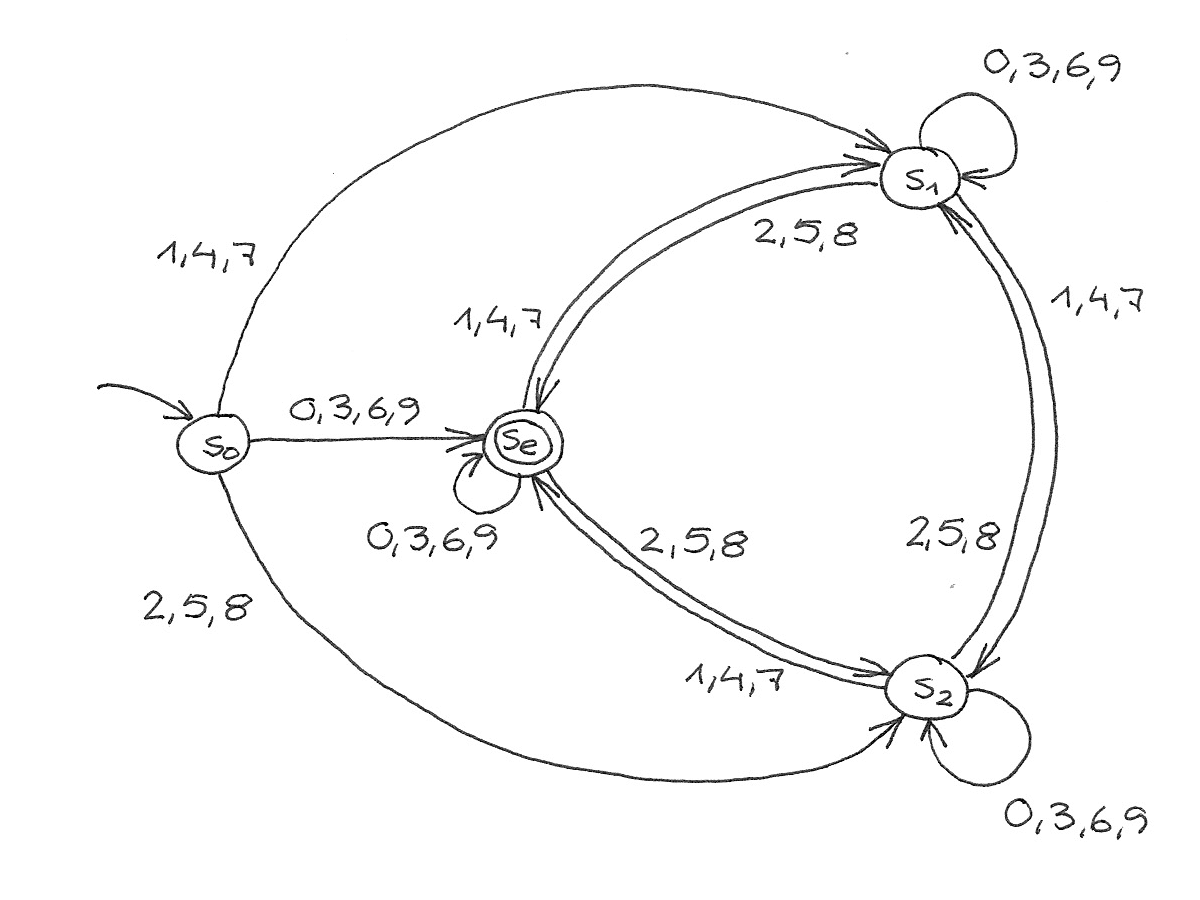
Analog zum 3er gibt’s auch bei der Teilbarkeit durch 9 einen Ring, in dem man mit 1 in den jeweils nächsten Zustand in eine Richtung (in meinem Diagramm in Uhrzeigerrichtung) kommt und mit 9 − 1 = 8 in die andere. Mit 0 und 9 verbleibt man im jeweiligen Zustand; mit den anderen Ziffern nimmt man Abkürzungen über die Diagonalen:

(Die nahe am Zustand stehenden Symbole geben die Richtung an, wie man aus dem Zustand rauskommt; die Pfeile und doppelten Linien hab ich gespart.)

‚Aber Gunnar‘, werdet ihr sagen, ‚Anfangs- und Endzustand müssen doch aufgedröselt sein!‘

„Marty, du musst vierdimensional denken!“ Hier reicht eine weniger, wie dedlfix sagte: „Denk mal dreidimensional.“

Hab ich gemacht und in 3D gezeichnet: Anfangs- und Endzustand befinden sich in der Projektion genau hintereinander und damit überlappen sich auch ihre Verbindungen zu den anderen Zuständen und deren identischen Beschriftungen! 😜 (Die Ausrede konnte ich nicht an andere verschenken, die brauchte ich für mich selber.)

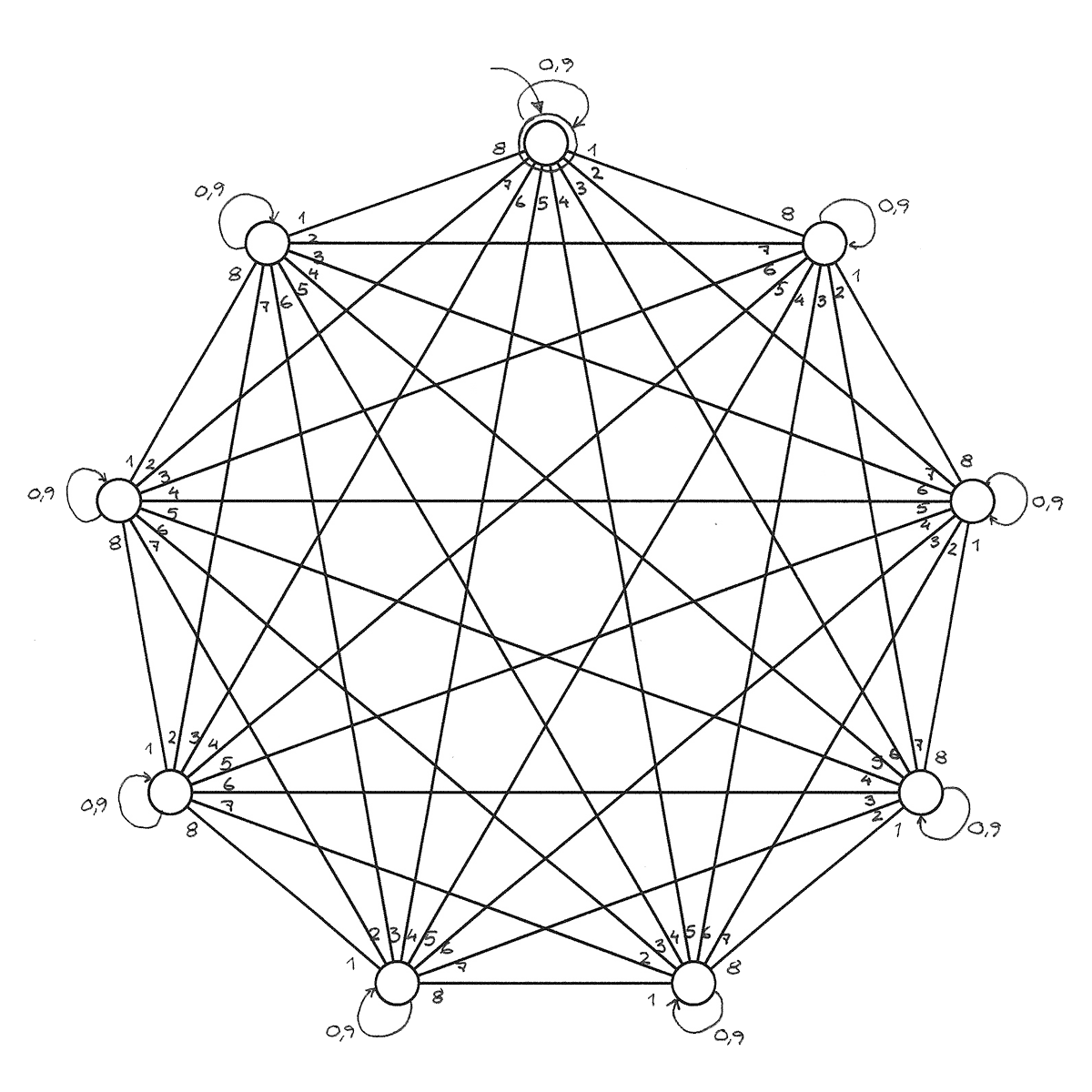
Das Neuneck mit Diagonalen hatte ich eigentlich für die Teilbarkeit durch 16 angedacht. Es liegt die Vermutung nahe, dass ein Automat dafür 9 Zustände braucht. Allgemein: 2ⁿ⁻¹ + 1 Zustände für die Teilbarkeit durch 2ⁿ.

Da ich faul bin, hatte ich nach einer Grafik eines Neunecks mit Diagonalen gesucht, aber nur eine in einer Auflösung unter 200 × 200 Pixel gefunden. Also selber machen. Da ich faul bin: machen lassen – von einem Script. Und dabei wieder was gelernt: createElement('path') geht nicht; es muss createElementNS('http://www.w3.org/2000/svg', 'path') mit Angabe des SVG-Namensraums sein.

(Neuneck als SVG und als in HTML eingebettetes SVG)

LLAP 🖖