Informatik zum Jahresanfang – noch mehr Teiler

[Gunnar Bittersmann]

@@Gunnar Bittersmann

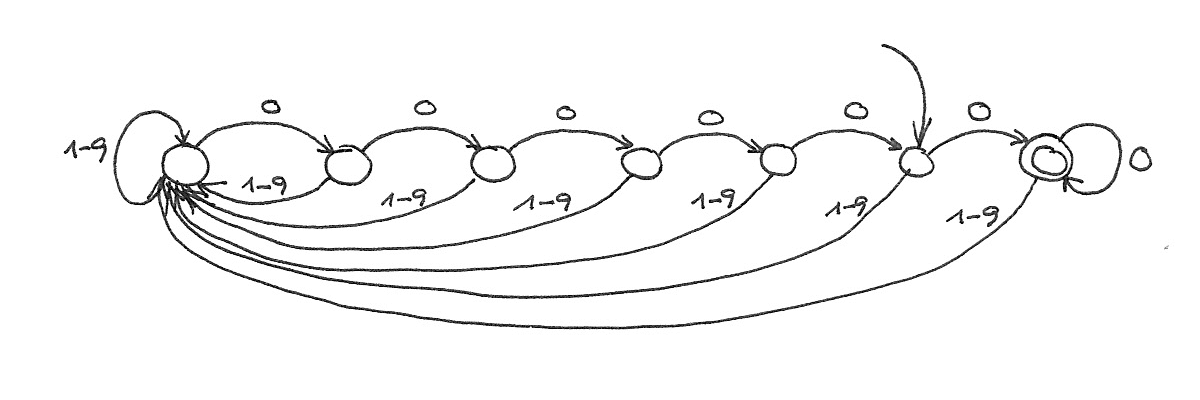
Der minimale Automat für die Teilbarkeit durch 10ⁿ lässt sich auch einfach formal beschreiben:

$$\begin{align} \text{Menge der Zustände:} \quad S &= {s_0, s_1, \ldots, s_n}
\text{Menge der Endzustände:} \quad F &= {s_n}
\text{Eingabealphabet:} \quad \Sigma &= {0, 1, 2, \ldots, 9}
\end{align}$$

[Ergänzung] Der Index des Zustands gibt die Anzahl der zuletzt in Folge gelesenen Nullen an.

$$\text{Übergangsfunktion:} \quad \delta(s_i, d) = \begin{cases} s_{i+1} & \text{ für } d = 0 \text{ und } i < n
s_n & \text{ für } d = 0 \text{ und } i = n
s_0 & \text{ für } d \ne 0
\end{cases}$$

Das schwerste hieran war wohl, den Startpfeil richtig zu setzen.

$$\text{Startzustand:} \quad s_{n-1}$$

LLAP 🖖