Hallo Matthias Apsel,
Das ist nicht begrenzt. Aber wenn ich es exakt beschreiben möchte, ist es schon fast keine Aufgabe mehr.
Das Thema scheint ausgelutscht zu sein. Ich führe deshalb mal aus, wie eine Zahl aufgebaut ist.
- sie beginnt mit einem Minuszeichen oder einer Ziffer
- das Minuszeichen darf nur am Anfang vorkommen
- sie hat höchstens ein Komma
- sie darf nicht mit dem Komma enden
- falls sie mit einer Null beginnt, folgt nichts oder ein Komma
- Gunnar hat in seiner an die Jahreszeit angepasste Lösung noch mit Nullen endende Nachkommaanteile verboten
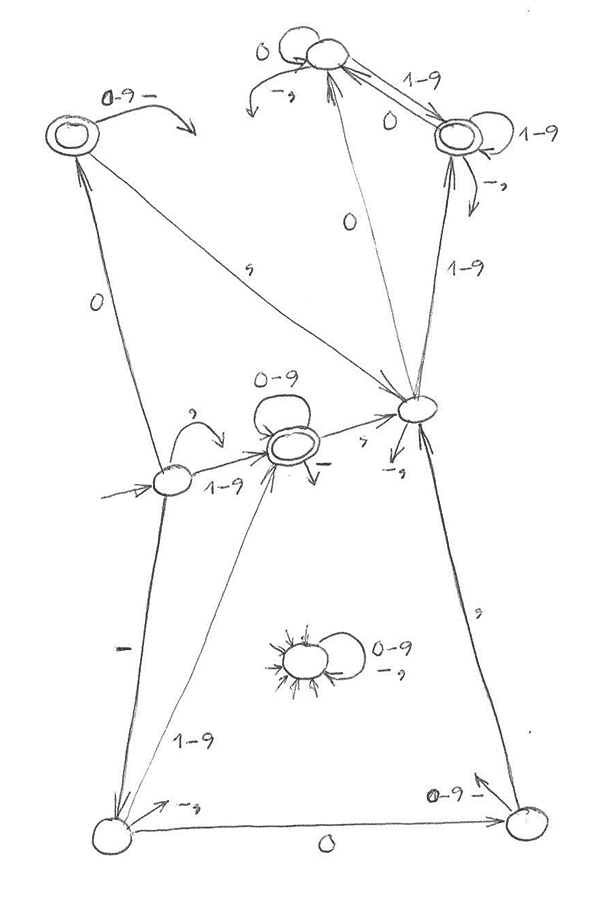
Die Pfeile ins Nirwana führen in den Nebel.
Und ob eine Zahl gültig ist, wird meiner Meinung nach von allen Interpretern auf diese Weise geprüft. Wobei die Kriterien sich durchaus unterscheiden können. In manchen CAS beispielsweise ist 2. eine gültige Zahl und im Unterschied zu 2 ein Näherungswert und das Programm anweist, mit Näherungswerten zu rechnen.
solve(x^2=2.,x) // x=1,414213562373095 or x=-1,414213562373095
solve(x^2=2,x) // x=√2 or x=-√2
Bis demnächst
Matthias
--
Pantoffeltierchen haben keine Hobbys.
Pantoffeltierchen haben keine Hobbys.


