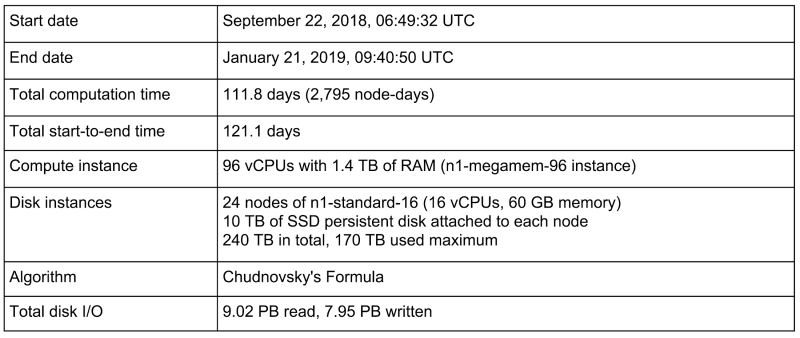
Google hat 2795 Node-Days (112 Tage auf 96 vCPUs) gebraucht.(Die 24 Speichergeräte mit je 16 CPUs, 60GB Ram und 10 TB Plattenspeicher sind da wohl nicht mitgerechnet...)
Errechnete π-Stellen von Google vers. Anzahl voraussichtlicher Versuche, alle 32 Stellen eines Passcodes aus Ziffern zu erraten:
31415926535897
50000000000000000000000000000000
Ich lasse bei der folgenden Aussage mal die Unterschiede zwischen den Berechnungen selbst grob fahrlässig außer acht, 32-Ziffern-Passwort-Knacken dauert also mit aktueller Technik sehr grob geschätzt 1000000000000000000 mal länger. Also:
3.000.000.000.000.000.000.000 Node-Days.
Doch Vorsicht.
Mit einer großen Menge in der Masse billigen Asics, die nur Hasches nach genau einem Algo berechnen können (Mit sowas könnte man auch weitere Stellen von π deutlich schneller berechnen und mit sowas werden auch Bitcoins geerntet), könnte man das Passwort-Knacken sehr stark parallelisieren und die einen oder anderen 3 Stellen der "Node-Days" abknapsen. Ich würde sagen, 3 Milliarden Tage sind absolut realistisch. Allerdings auch wieder nicht, weil sich die Rechenleistung innerhalb dieses Zeitrahmens dramatisch erhöht und die Zeitdauer also dramatisch verringert: Nach jeweils 500 Tagen würde man für den Rest nur noch halb so lange brauchen...
 Gunnar Bittersmann
Gunnar Bittersmann
 TS
TS
 Rolf B
Rolf B
 dedlfix
dedlfix
Tabellenkalk
 dedlfix
dedlfix
 TS
TS



