nicht angemeldet
Hallo in die Runde,
ich versuche mal, das Ganze etwas anschaulicher zu machen.
Das "Zufallsexperiment" soll aber aus dem 4-maligen Werfen eines Würfels bestehen.
(17 oder 24 Würfe darzustellen wäre doch etwas unhandlich.)
Wir notieren einen einzelnen Wurf als 1 (= Treffer = Sechs) bzw. 0 (= Niete = keine Sechs),
und den Ausgang eines viermaligen Werfens als geordnetes "4-Tupel", z.B.
0010
(nur der 3. Wurf war eine Sechs).
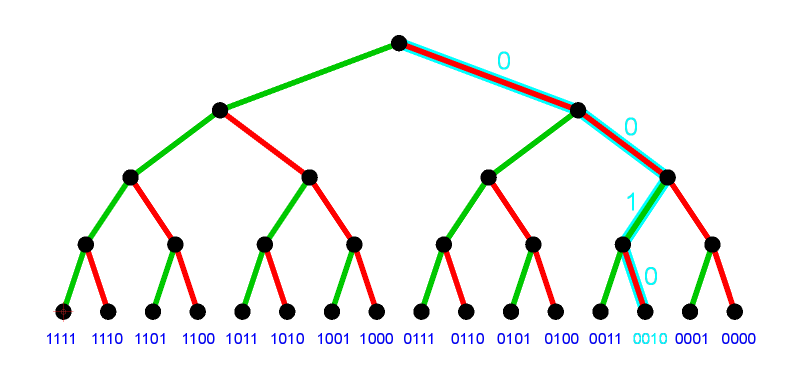
Es gibt 16 mögliche Ausgänge des Experiments, die sich gut in einem Baumdiagramm darstellen lassen:
Jeder Ausgang des Experiments entspricht einem "Pfad" in diesem Baum, von der Wurzel (oben) in 4 Schritten nach unten. Grüne Schritte sind Treffer, rote sind Nieten.
Da wir faire Würfel voraussetzen, beträgt bei jedem Schritt die Wahrscheinlichkeit für grün 1/6 und für rot 5/6.
Es gelten zwei Pfadregeln.
Pfadregel 1:
Die Wahrscheinlichkeit für einen bestimmten Pfad
ist das Produkt der Wahrscheinlichkeiten der einzelnen Schritte.
Der Pfad 0010 hat also die Wahrscheinlichkeit
$$\frac{5}{6}\cdot\frac{5}{6}\cdot\frac{1}{6}\cdot\frac{5}{6}=(\frac{5}{6})^3\cdot\frac{1}{6}=\frac{5^3}{6^4}=0,096= 9,6$$%.
(Kurzschreibweise: $$Wk(0010)=\frac{5^3}{6^4}$$.)
Wir interessieren uns für die Wahrscheinlichkeiten bestimmter Ereignisse, die beim 4-maligen Werfen eines Würfels auftreten können. Ein Ereignis ist mathematisch durch die Menge der Pfade definiert, bei denen es eintritt.
Beispiele:
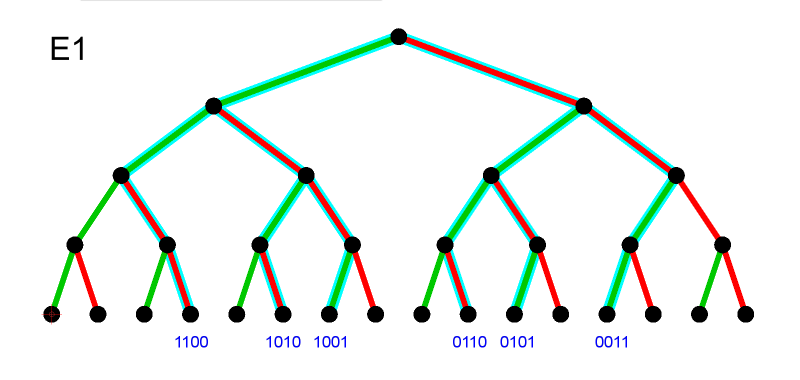
Ereignis E1: "Es fällt genau 2-mal die Sechs."
Zu diesem Ereignis gehören die 6 Pfade
1100
1010
1001
0110
0101
0011
Jeder dieser Pfade hat die gleiche Wahrscheinlichkeit $$(\frac{1}{6})^2\cdot(\frac{5}{6})^2=\frac{25}{1296}=0,019=1,9$$%.
Nun brauchen wir die
Pfadregel 2:
Die Wahrscheinlichkeit eines Ereignisses ist die Summe der Wahrscheinlichkeiten der zu ihm gehörenden Pfade.
Da bei E1 die 6 Summanden gleich sind, brauchen wir nur zu multiplizieren:
$$Wk(E1)=6 \cdot(\frac{1}{6})^2\cdot(\frac{5}{6})^2=\frac{25}{216}=0,116=11,6$$%.
(Kleine Probeaufgabe: Man rechne nach, dass sich die Wahrscheinlichkeiten aller 16 Pfade
zu 1 = 100% addieren.)
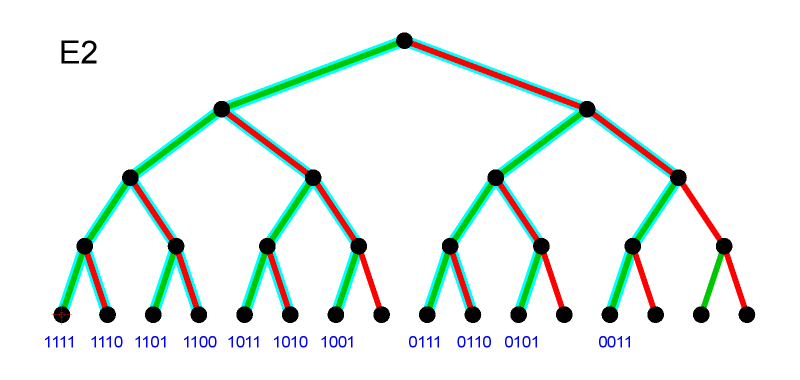
Ereignis E2: "Es fällt mindestens 2-mal die Sechs."
Hier kommen zu den 6 Pfaden von E1 noch 4 Pfade mit 3 Sechsen
1110
1101
1011
0111
sowie der eine Pfad mit 4 Sechsen hinzu:
1111
Wir erhalten $$Wk(E2)=Wk(E1)+4\cdot(\frac{1}{6})^3\cdot\frac{5}{6}+(\frac{1}{6})^4=\frac{150+20+1}{6^4}=\frac{171}{1296}=0,132 =13,2$$%.
Ereignis E3: "Es fällt mindestens eine Sechs."
Alle Pfade enthalten mindestens einen grünen Schritt, mit Ausnahme des letzten, der ganz rot ist.
Deshalb liegt es nahe, das Gegenereignis von E3 zu betrachten - das eben nur aus diesem einen Pfad besteht ("Es fällt keine Sechs"):
$$Wk(0000)=(\frac{5}{6})^4=0,482=48,2$$%.
Wegen der 2. Pfadregel folgt
$$Wk(E3)=1-(\frac{5}{6})^4=0,518=51,8$$%.
Es wäre also günstig, darauf zu wetten, dass mindestens eine Sechs fällt.
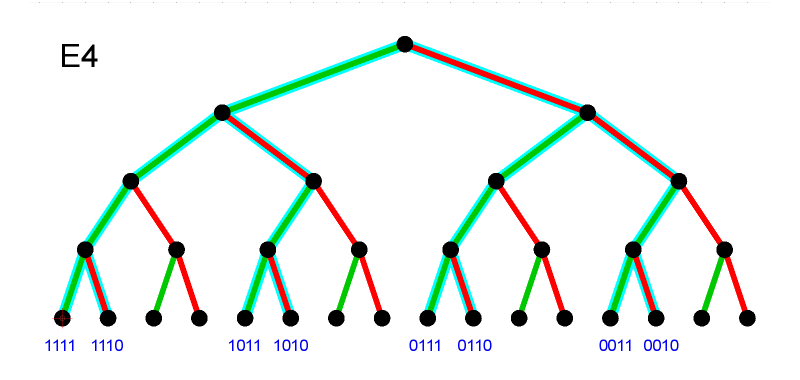
Ereignis E4: Der dritte Wurf ist eine Sechs."
Es gibt 8 Pfade zu E4:
1111
1110
1011
1010
0111
0110
0011
0010
Je einer davon hat 4 Treffer bzw. einen Treffer, und je drei davon haben 3 Treffer bzw. 2 Treffer.
Damit errechnen wir
$$Wk(E4)=(\frac{1}{6})^4+3\cdot(\frac{1}{6})^3\cdot(\frac{5}{6})^1+3\cdot(\frac{1}{6})^2\cdot(\frac{5}{6})^2+(\frac{1}{6})^1\cdot(\frac{5}{6})^3$$ $$=\frac{1+15+75+125}{6^4}=\frac{216}{6^4}=\frac{6^3}{6^4}=\frac{1}{6}$$
Man erhält also für das Ereignis, dass der dritte Wurf eine Sechs ist, die Wahrscheinlichkeit 1/6
– welchen Ausgang die anderen 3 Würfe haben, spielt keine Rolle!
Viele Grüße! ottogal
Henry
Der Martin
Gunnar Bittersmann
Tabellenkalk
Rolf B