nicht angemeldet
Mathematik zur Wochenmitte
Gunnar Bittersmann
Mathematik zur Wochenmitte
Gunnar Bittersmann
Matthias Apsel
Tabellenkalk
Rolf BJetzt aber: die versprochene Aufgabe von Catriona Shearer.
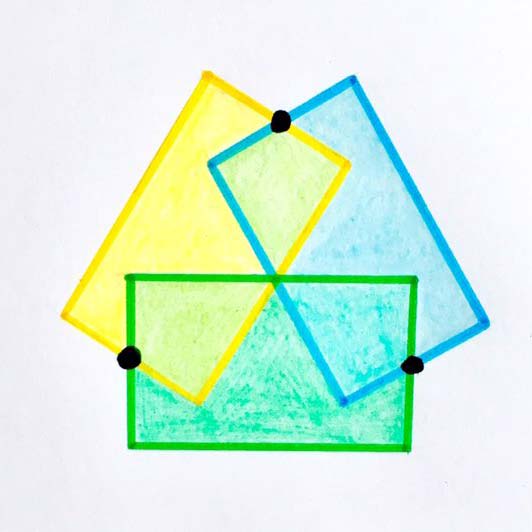
Die drei sich überlappenden Rechtecke sind kongruent und haben jeweils den Flächeninhalt 4. Die markierten Punkte sind die Mittelpunkte der kürzeren Seiten. Wie groß ist der von dieser Figur abgedeckte Flächeninhalt?
LLAP 🖖
--
„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“ —Kurt Weidemann
„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“ —Kurt Weidemann
-
Hallo Gunnar Bittersmann,
Die drei sich überlappenden Rechtecke sind kongruent und haben jeweils den Flächeninhalt 4. Die markierten Punkte sind die Mittelpunkte der kürzeren Seiten. Wie groß ist der von dieser Figur abgedeckte Flächeninhalt?
Mir scheint, da fehlt noch was. Schneiden sich die drei Rechtecksseiten in genau einem Punkt?
Bis demnächst
Matthias--
Pantoffeltierchen haben keine Hobbys.-
Hallo,
Mir scheint, da fehlt noch was. Schneiden sich die drei Rechtecksseiten in genau einem Punkt?
Catriona Shearer tweeetete:
That is required - it’s not stated but hopefully obvious from the diagram
Gruß
Kalk -
@@Matthias Apsel
Mir scheint, da fehlt noch was. Schneiden sich die drei Rechtecksseiten in genau einem Punkt?
Ja, das ist wohl im Sinne der Aufgabe.
Ich hatte das erst übersehen und drauflosgerechnet … Könnt Ihr auch gerne als Zusatzaufgabe machen. (Da sollte dann sowas wie das Seitenverhältnis als Parameter im Ergebnis vorkommen.)
LLAP 🖖
--
„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“ —Kurt Weidemann-
Hallo Gunnar,
Könnt Ihr auch gerne als Zusatzaufgabe machen.
Das wird aber in Arbeit ausarten, ich identifiziere 5 Varianten mit eigenen Rechenwegen
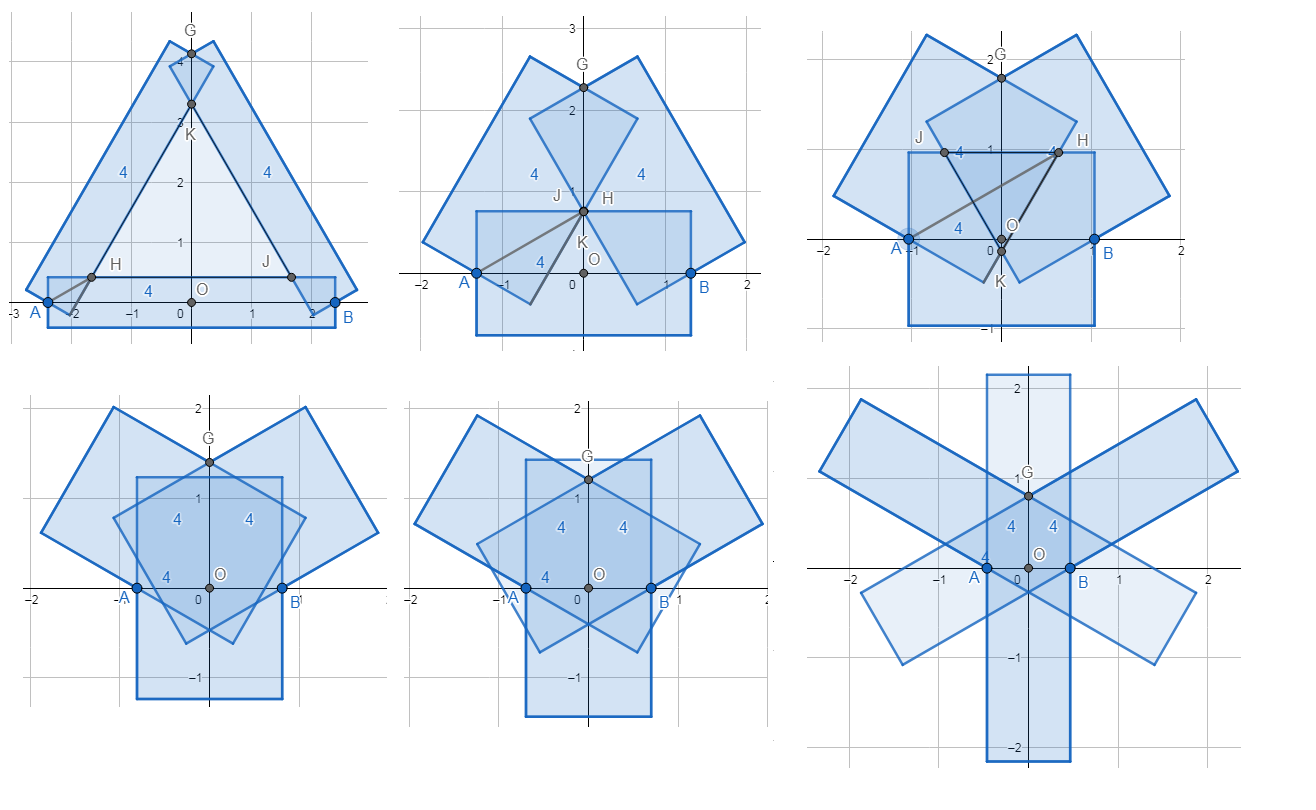
Catrionas Aufgabe (oben mitte) sollte ein Sonderfall von oben links oder oben rechts sein.
Rolf
--
sumpsi - posui - clusi-
Hallo,
ich identifiziere 5 Varianten mit eigenen Rechenwegen
Die untere Reihe gilt nicht. Aufgabe nicht gelesen?
Gruß
Kalk-
Hallo Tabellenkalk,
was habe ich überlesen? Es geht ja um Gunnars Zusatzaufgabe, bei der der Schnitt dreier Rechteckseiten im Zentrum aufgehoben ist.
Catrionas Aufgabe ist nur die oben in der Mitte, und die ist nach kurzem Nachdenken trivial.
Rolf
--
sumpsi - posui - clusi-
Hallo,
was habe ich überlesen?
Das mit der kurzen Seite.
Es geht ja um Gunnars Zusatzaufgabe, bei der der Schnitt dreier Rechteckseiten im Zentrum aufgehoben ist.
Von der kurzen Seite hat Gunnar gar nicht gesprochen.
Gruß
Kalk-
Hallo Tabellenkalk,
ok, einverstanden. Aber berechenbar sind die Fälle trotzdem :)
Rolf
--
sumpsi - posui - clusi-
Hallo,
Aber berechenbar sind die Fälle trotzdem :)
berechenbar ist Vieles… 😉
@Gunnar Bittersmann: Drauflosrechnen führt meistens zum Ergebnis für eine nichtgestellte Aufgabe!
Gruß
Kalk-
@@Tabellenkalk
Drauflosrechnen führt meistens zum Ergebnis für eine nichtgestellte Aufgabe!
„Richtige Antwort, Hoëcker. Nur auf eine völlig andere Frage.“
LLAP 🖖
--
„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“ —Kurt Weidemann-
Hallo,
„Richtige Antwort, Hoëcker. Nur auf eine völlig andere Frage.“
Wieso DAS denn?
Gruß
Kalk
-
-
-
-
-
Hallo Rolf B,
Catrionas Aufgabe ist nur die oben in der Mitte, und die ist nach kurzem Nachdenken trivial.
Ja, und ich wollte so gern wissen, wie groß die Seiten sind. 😂
Bis demnächst
Matthias--
Pantoffeltierchen haben keine Hobbys.-
Hallo Matthias,
kann ich Dir sagen:
$$a = \frac{2}{\sqrt {\tan{30^\circ} }} = 2 \sqrt[4]{3}\ b = \frac 4 a$$
Urgh, ist das klein. a ist zweimal die vierte Wurzel von drei.
Rolf
--
sumpsi - posui - clusi
-
-
-
-
-
-
-
@@Gunnar Bittersmann
Wenn man nicht übersieht, dass sich die „inneren“ Rechteckseiten in einem Punkt schneiden, war die Aufgabe nicht allzu schwer. Niemand (außer mir 😆) hat sich da aufs Glatteis führen lassen und mit Wurzeln oder sowas rumgerechnet.
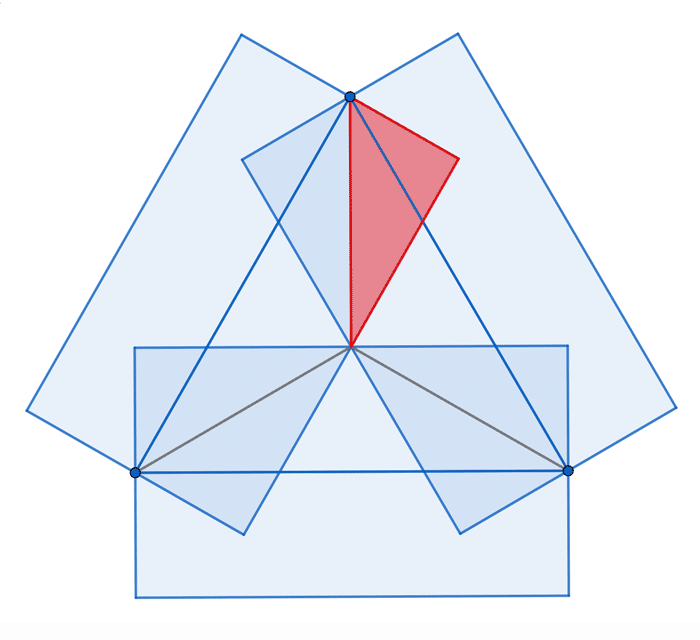
Von den 3 Rechteckflächen Aᵣ muss man 6 rechtwinklige Dreiecke abziehen, deren Flächeninhalt ⅛Aᵣ beträgt. 3Aᵣ − ⁶⁄₈Aᵣ = 2¼Aᵣ = 9.
Die meisten haben’s mit Mythologie und mir noch ein Märchen mit Drachen erzählt.
@ottogal hat auch den allgemeinen Fall durchgerechnet, d.h. beide Fälle. Mit Seitenlängen[1] a ≥ b
$$A = \begin{cases} 3ab - \frac{3}{4}b^2 \sqrt{3}, & \text{wenn }a ≥ b \sqrt{3}
\frac{3}{2}ab + \frac{1}{4}a^2 \sqrt{3}, & \text{wenn }b ≤ a < b \sqrt{3} \end{cases}$$(Für a = b√3 kommt beides aufs selbe raus, d.h. die Funktion A(a, b) ist stetig. Ottogal hat auch noch gezeigt, dass sie an der Übergangsstelle keinen Knicks macht, also stetig differenzierbar ist.)
LLAP 🖖
--
„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“ —Kurt Weidemann
Ich habe die Variablen etwas umbenannt. ↩︎
-
Hallo alle,
In welchem Verhältnis müssen die Seitenlängen der Rechtecke stehen, damit man sie überhaupt wie gefordert übereinanderlegen kann?
Bis demnächst
Matthias--
Pantoffeltierchen haben keine Hobbys.-
@@Matthias Apsel
In welchem Verhältnis müssen die Seitenlängen der Rechtecke stehen, damit man sie überhaupt wie gefordert übereinanderlegen kann?
Ist die Frage nicht durch das Posting beantwortet, auf das du geantwortet hast?
LLAP 🖖
--
„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“ —Kurt Weidemann-
Hallo Gunnar Bittersmann,
In welchem Verhältnis müssen die Seitenlängen der Rechtecke stehen, damit man sie überhaupt wie gefordert übereinanderlegen kann?
Ist die Frage nicht durch das Posting beantwortet, auf das du geantwortet hast?
Ist sie, nur nicht in schön. Ich war überrascht, wie einfach das geht.
Bis demnächst
Matthias--
Pantoffeltierchen haben keine Hobbys.-
@@Matthias Apsel
Ich war überrascht, wie einfach das geht.
Die Hälfte der kurzen Seite b ist gleich dem Inkreisradius (gleich einem Drittel der Höhe) im gleichseitigen Dreieck mit der Seitenlänge a. Oder geht’s noch einfacher?
LLAP 🖖
--
„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“ —Kurt Weidemann-
Hallo Gunnar Bittersmann,
Die Hälfte der kurzen Seite b ist gleich dem Inkreisradius (gleich einem Drittel der Höhe) im gleichseitigen Dreieck mit der Seitenlänge a.
Das war meine erste Idee.
Oder geht’s noch einfacher?
Wesentlich. Vor allem, wenn nach dem Seitenverhältnis gefragt ist.
Bis demnächst
Matthias--
Pantoffeltierchen haben keine Hobbys.-
@@Matthias Apsel
Oder geht’s noch einfacher?
Wesentlich. Vor allem, wenn nach dem Seitenverhältnis gefragt ist.
Hm, Pythagoras? b² = ⅓a²
Oder geht’s noch einfacher?
LLAP 🖖
--
„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“ —Kurt Weidemann-
Hallo Gunnar Bittersmann,
Oder geht’s noch einfacher?
3_ab_ = _a_²√3
Bis demnächst
Matthias--
Pantoffeltierchen haben keine Hobbys.-
Hallo Matthias Apsel,
3_ab_ = _a_²√3
Begründung:
Klappt man die „Überlappungen“ nach außen, so entsteht ein gleichseitiges Dreieck mit der Seitenlänge 2_a_. Dies ist flächengleich den drei Rechtecken.
Aus 3_ab_ = _a_²√3 folgt dann unmittelbar a : b = √3 : 1 oder _a_² : _b_² = 3 : 1.
Bis demnächst
Matthias--
Pantoffeltierchen haben keine Hobbys.
-
-
-
-
-
-
-
-
@ottogal hat auch den allgemeinen Fall durchgerechnet, d.h. beide Fälle. Mit Seitenlängen[1] a ≥ b
$$A = \begin{cases} 3ab - \frac{3}{4}b^2 \sqrt{3}, & \text{wenn }a ≥ b \sqrt{3}
\frac{3}{2}ab + \frac{1}{4}a^2 \sqrt{3}, & \text{wenn }b ≤ a < b \sqrt{3} \end{cases}$$(Für a = b√3 kommt beides aufs selbe raus, d.h. die Funktion A(a, b) ist stetig. Ottogal hat auch noch gezeigt, dass sie an der Übergangsstelle keinen Knicks macht, also stetig differenzierbar ist.)
Genauer: Die bei konstantem $$b$$ definierte Funktion
$$A(a) = \begin{cases} 3ab - \frac{3}{4}b^2 \sqrt{3}, & \text{wenn }a ≥ b \sqrt{3}
\frac{3}{2}ab + \frac{1}{4}a^2 \sqrt{3}, & \text{wenn }b ≤ a < b \sqrt{3} \end{cases}$$ist an der Übergangsstelle $$b \sqrt{3}$$ stetig und differenzierbar (nach $$a$$).
(Bem.: Die folgende Fußnote gehört eigentlich zum Zitat.)
Ich habe die Variablen etwas umbenannt. ↩︎