Mathematik zur Wochenmitte – Lösung

[Gunnar Bittersmann]

@@Gunnar Bittersmann

Wenn man nicht übersieht, dass sich die „inneren“ Rechteckseiten in einem Punkt schneiden, war die Aufgabe nicht allzu schwer. Niemand (außer mir 😆) hat sich da aufs Glatteis führen lassen und mit Wurzeln oder sowas rumgerechnet.

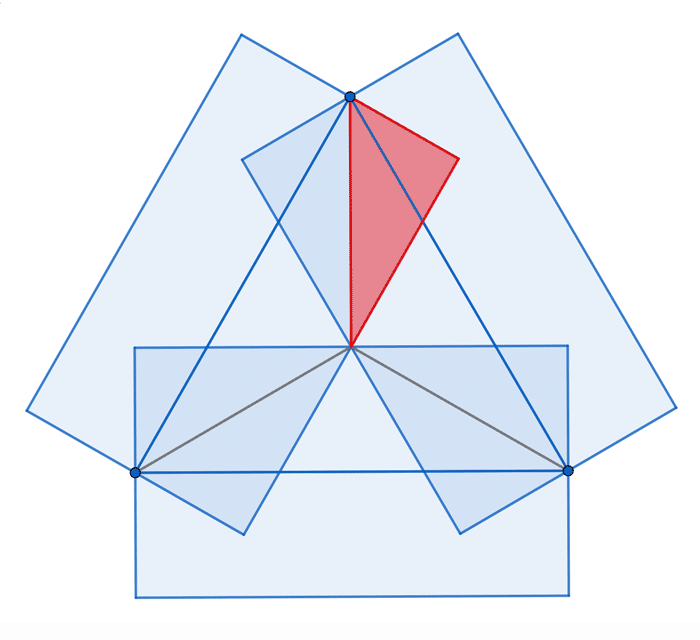
Von den 3 Rechteckflächen Aᵣ muss man 6 rechtwinklige Dreiecke abziehen, deren Flächeninhalt ⅛Aᵣ beträgt. 3Aᵣ − ⁶⁄₈Aᵣ = 2¼Aᵣ = 9.

Die meisten haben’s mit Mythologie und mir noch ein Märchen mit Drachen erzählt.

@ottogal hat auch den allgemeinen Fall durchgerechnet, d.h. beide Fälle. Mit Seitenlängen^[1] a ≥ b

$$A = \begin{cases} 3ab - \frac{3}{4}b^2 \sqrt{3}, & \text{wenn }a ≥ b \sqrt{3}
\frac{3}{2}ab + \frac{1}{4}a^2 \sqrt{3}, & \text{wenn }b ≤ a < b \sqrt{3} \end{cases}$$

(Für a = b√3 kommt beides aufs selbe raus, d.h. die Funktion A(a, b) ist stetig. Ottogal hat auch noch gezeigt, dass sie an der Übergangsstelle keinen Knicks macht, also stetig differenzierbar ist.)

LLAP 🖖

---

1. Ich habe die Variablen etwas umbenannt. ↩︎