nicht angemeldet ottogal
Rolf B
ottogal
Gunnar Bittersmann
ottogal
ottogal
Rolf B
Gunnar Bittersmann
E und F sind Seitenmitten des Quadrats ABCD.
Man berechne jeweils den Flächenanteil der farbigen Dreiecke an der Quadratfläche.
Hallo ottogal,
ADH ist geschenkt, das hatten wir ja bei Gunnars Aufgabe zum Wochenende dabei. Ich zumindest 😀
Rolf
Eben, zum Aufwärmen eben erst was Vertrautes. Laut Gunnar ist dein Vorgehen elegant... 😉
@@ottogal
Man berechne jeweils den Flächenanteil der farbigen Dreiecke an der Quadratfläche.
Da gibt’s wieder Einschränkungen, wie man das (nicht) tun sollte? Die Koordinaten von G und H wären einfach berechnet, dann wäre man schon fertig.
LLAP 🖖
Eben, nur was zum Aufwärmen. Soll ja auch bis Dienstagmittag vom Tisch sein.
Am Nachmittag kommt dann was Handfesteres...
@@ottogal
Da gibt’s wieder Einschränkungen, wie man das (nicht) tun sollte? Die Koordinaten von G und H wären einfach berechnet
Pah, geht auch ohne!
dann wäre man schon fertig. Eben, nur was zum Aufwärmen.
Eben nicht. Bei der Berechnung von △HGE hat man – bei Kantenlänge 1 des Quadrats – dann (zwischenzeitlich) Wurzeln – und das auch noch mit Brüchen, und das gar mit drei(!)stelligen Nennern!
Ich stelle die Aufgabe mal wie die anderen: Finde die Lösung ohne Pythagoras, Wurzeln oder Trigonometrie.
Die „geschenkte“ Fläche von △ADH ist dabei hilfreich; ebenso die entscheidende Hilfslinie. (Andere Hilfslinien ergeben sich dann von selbst.)
LLAP 🖖
Hallo Gunnar,
hab ich doch schon längst. 1/5, 1/12 und 1/30. Rechenweg liegt Ottogal vor 😀
Rolf
@@Rolf B
Rechenweg liegt Ottogal vor 😀
Rechenweg?
LLAP 🖖
Hallo Gunnar,
sicher, ich könnte natürlich auch $$\frac{1}{12}-\frac{1}{20}$$ als Fläche von GHE stehen lassen. Die Fläche irgendwie direkt abzulesen - dafür bin ich zu blöd.
Und ein paar Worte zu verlieren, weshalb man diese mit jener Zahl kombiniert, macht sich immer gut. Nennen wir es also Kurzreferat.
Rolf
So, der Dienstagmittag ist verstrichen. Ich will es Rolf überlassen, ob er seine Lösung hier zeigen will. Die Wurzelrechnung von Gunnar hätte mich aber auch noch interessiert...
Hier meine Lösung:
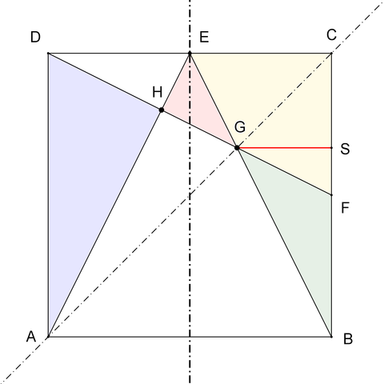
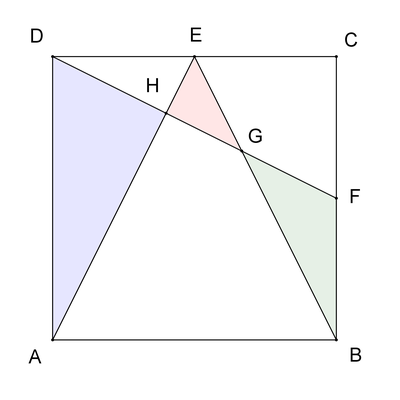
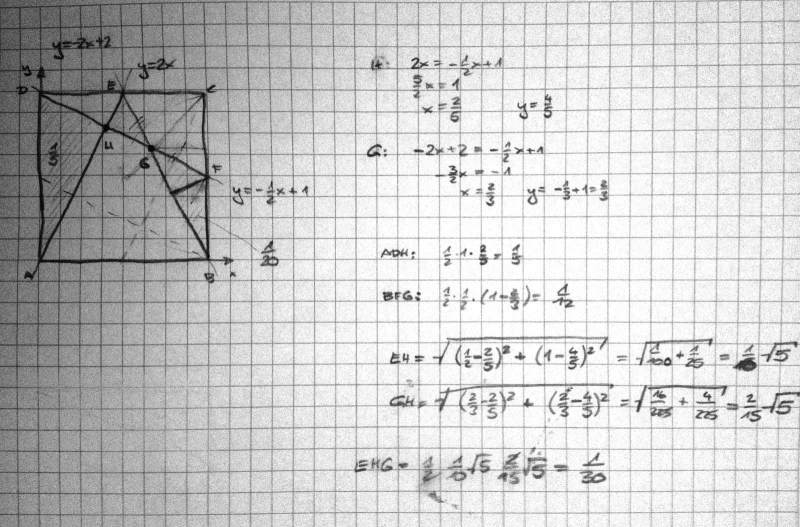
Wieder sei o.B.d.A. die Quadratseite 1.
Bekanntlich sind die Teildreiecke ADH und DEH des rechtwinkligen Dreiecks AED zu diesem ähnlich und haben daher auch dessen Kathetenverhältnis 2:1.
Daraus folgt HE:HD:HA = 1:2:4 und damit AH:AE = 4:5.
Die Dreiecke AHD und AED haben gleiche Höhe DH, ihre Flächen verhalten sich daher wie die dazugehörigen Grundseiten:
A(AHD):A(AED)=AH:AE = 4:5
Da A(AED) ein Viertel der Quadratfläche 1 ist, folgt also
A(AHD) = 4/5 A(AED) = (4/5)(1/4) = 1/5.
Entsprechend ist A(HED):A(AED) = 1:5, also
A(HED) = (1/5)(1/4) = 1/20.
Wegen der Symmetrie zur Achse AC sind die Dreiecksflächen A(CEG) und A(CFG) gleich; letztere ist aber gleich A(BFG), da die Grundseiten CF und BF gleich sind und sie die Höhe GS gemeinsam haben. Diese drei Dreiecke haben daher jeweils 1/3 der Fläche von Dreieck BCE, welche 1/4 beträgt. Somit ist
A(BFG) = 1/12.
Wegen der Symmetrie ist daher auch A(DEG) = 1/12, und man erhält
A(HEG) = A(DEG) - A(DEH) = 1/12 - 1/20 = 1/30.
Viele Grüße
ottogal
Hallo,
die Berechnung für die Fläche von DEH habe ich einfach aus Gunnars Aufgabe abgegriffen und nicht mehr aufgeschrieben.
Für den Rest hatte ich es mir etwas umständlicher gemacht und ein paar Linien mehr gezeichnet.
Wegen der Parallelität der roten Linien kann man den Strahlensatz verwenden, um zu zeigen, dass G die Strecke LC und L die Strecke AG in der Mitte teilt, also L und G die Strecke AC dritteln. G liegt also bei (2/3, 2/3). Daraus folgt, dass die Dreiecke EDG und BFG eine Höhe von 1/3 haben, die Grundseite von 1/2 ist klar, woraus dann die Fläche von 1/12 folgt.
Die Berechnung von HGE hatte ich zuerst VIEL zu umständlich; ich war von CDF ausgegangen und habe GFC, CEG und EDH davon abgezogen - dabei ist mir natürlich NICHT aufgefallen, dass GFC, CEG und BFG gleich groß sind und damit Ottogals "geteilt durch 3" Trick möglich ist. Grrr. Im zweiten Schritt habe ich dann erkannt, dass BFG und DEG punktsymmetrisch bezüglich G sind (was Ottogal zu einem müden Achsenzucken bewegte) und damit war ich dann auch bei 1/12-1/20.
Rolf
@@ottogal
Die Wurzelrechnung von Gunnar hätte mich aber auch noch interessiert...
Hier meine Lösung:
Ah ja, so geht’s auch.
Meine Hilfslinie war das Lot von F auf BG, Fußpunkt sei J.
KL Parallele zu DC durch G.
Fläche von △ADH ist ⅕. Geschenkt.
Wegen der Symmetrie (E in der Mitte von DC) sind △BFJ und △ADH ähnlich. BF = ½; △BFJ ist demnach halb so groß wie △ADH; seine Fläche ist ein Viertel so groß, also ⅟₂₀.
Nach Winkelhalbierendensatz teilt die Winkelhalbierende CG die Seite DF im Verhältnis DG : GF = DC : CF = 2 : 1. Nach Strahlensatz ist dann auch KG : GL = 2 : 1, also GL = ⅓.
Die Fläche von △BFG ist ½ × ½ × ⅓ = ⅟₁₂.
Die Fläche von △FJG ist ⅟₁₂ − ⅟₂₀ = ⅟₃₀.
Wegen der Symmetrie an der Diagonalen AC (G liegt auf ihr) sind △EGH und △FJG kongruent, also ist auch ist auch die Fläche von △EGH gleich ⅟₃₀.
LLAP 🖖
Hallo Gunnar,
Nach Winkelhalbierendensatz teilt die Winkelhalbierende CG die Seite DF im Verhältnis DG : DF = DC : CF = 2 : 1. Nach Strahlensatz ist dann auch KG : GL = 2 : 1, also GL = ⅓.
Was du wieder alles ausgräbst... den kannte ich überhaupt nicht mehr. Du hast aber DG : GF gemeint, gelle?
Rolf
@@Rolf B
Nach Winkelhalbierendensatz teilt die Winkelhalbierende CG die Seite DF im Verhältnis DG : DF = DC : CF = 2 : 1.
Was du wieder alles ausgräbst... den kannte ich überhaupt nicht mehr.
Ich kannte den gar nicht. (Oder ich hatte ihn längst vergessen.)
Ich musste irgendwie an die Höhe GL rankommen. Hach, wäre doch schön, wenn sich dass auch 2 : 1 verhalten würde … CG ist Winkelhalbierende – was gilt denn dann? In der Wikipedia nachgeschlagen – und Glück gehabt.
Du hast aber DG : GF gemeint, gelle?
Klar. Berichtigt.
LLAP 🖖
Hallo Gunnar,
ok, ich hatte das über die roten Parallelen und Strahlensatz ermittelt; möglicherweise läuft das irgendwie auf einen Beweis des Winkelhalbierendensatzes hinaus. Keine Ahnung, keine Lust zum Forschen...
Rolf
Nett - danke Gunnar. Geometrische Beweisführungen sind doch irgendwie attraktiver als analytische.
Schön die Verwendung des Winkelhalbierende-Satzes; man müsste den viel öfter heranziehen.
Viele Grüße
ottogal
