nicht angemeldet
Gunnar Bittersmann@@ottogal
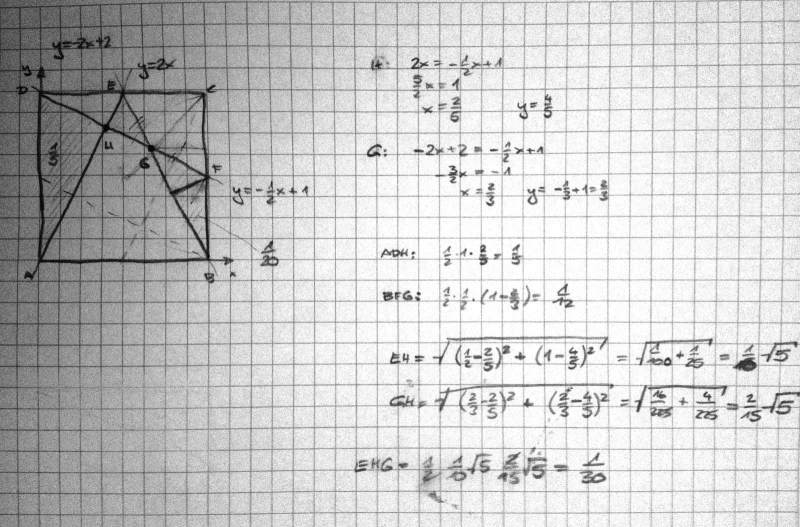
Die Wurzelrechnung von Gunnar hätte mich aber auch noch interessiert...
Hier meine Lösung:
Ah ja, so geht’s auch.
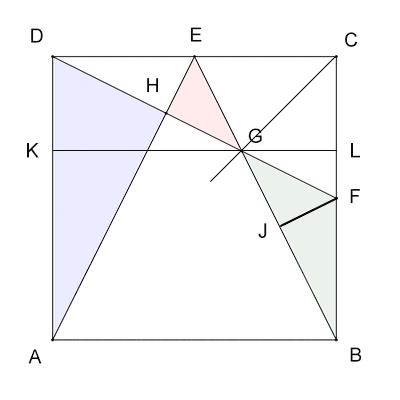
Meine Hilfslinie war das Lot von F auf BG, Fußpunkt sei J.
KL Parallele zu DC durch G.
Fläche von △ADH ist ⅕. Geschenkt.
Wegen der Symmetrie (E in der Mitte von DC) sind △BFJ und △ADH ähnlich. BF = ½; △BFJ ist demnach halb so groß wie △ADH; seine Fläche ist ein Viertel so groß, also ⅟₂₀.
Nach Winkelhalbierendensatz teilt die Winkelhalbierende CG die Seite DF im Verhältnis DG : GF = DC : CF = 2 : 1. Nach Strahlensatz ist dann auch KG : GL = 2 : 1, also GL = ⅓.
Die Fläche von △BFG ist ½ × ½ × ⅓ = ⅟₁₂.
Die Fläche von △FJG ist ⅟₁₂ − ⅟₂₀ = ⅟₃₀.
Wegen der Symmetrie an der Diagonalen AC (G liegt auf ihr) sind △EGH und △FJG kongruent, also ist auch ist auch die Fläche von △EGH gleich ⅟₃₀.
LLAP 🖖
„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“ —Kurt Weidemann
Rolf B