Mathematik zur Wochenmitte - Lösung

[Gunnar Bittersmann]

@@ottogal

Eine Gerade, die jedes der beiden Rechtecke halbiert, halbiert auch den Restkuchen.[…] Die Gerade, die die beiden Mittelpunkte verbindet, löst also die Aufgabe.

Das ist ja einfach!

Ich hatte was anderes im Sinn. (Hatte das nur in der Kürze der Zeit nicht aufgeschrieben. Du warst ja schnell mit der Auflösung.)

So gibt es stets eine vertikale Gerade, die das leistet. […] (Die lässt sich freilich nicht mehr geometrisch konstruieren, sondern nur numerisch approximieren.)

Hier wage ich zu widersprechen. Denn genau diese Gerade hatte ich im Sinn.

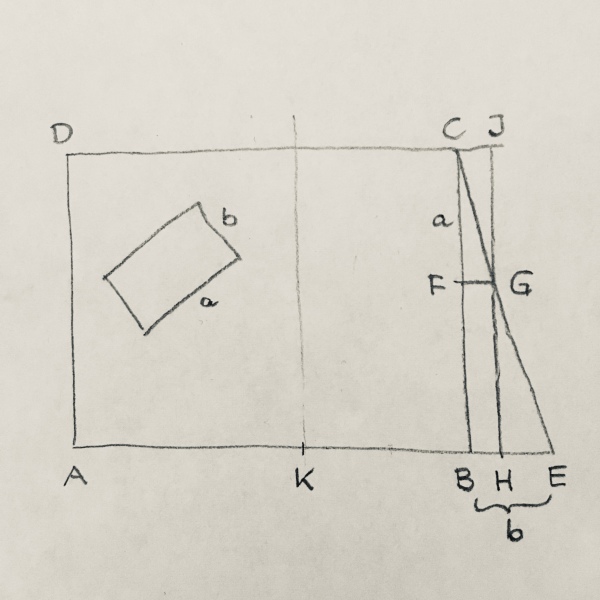
Die Seitenlängen des fehlenden Kuchenstücks seien a und b. (Dabei ist es egal, welches davon die längere Seite ist.)

Verlängere AB über B hinaus um b zum Punkt E. Wähle F auf BC so, dass CF = a.

Die Sekrechte zu BC durch F schneidet CE in G. Die Parallele zu BC durch G schneidet BE in H und CD in J.

Nach Strahlensatz ist nun FG : a = b : BC, folglich FG · BC = ab. Das Rechteck BHJC ist also genauso groß wie das fehlende Kuchenstück.

Sei K der Mittelpunkt von AH, d.h. die Senkrechte zu AB durch K teilt das Rechteck AHJD in zwei gleiche Teile.

Vom linken Teil schneiden wir das Kuchenstück heraus, vom rechten Teil das gleich große Stück BHJC – wir haben also ABCD wie gewünscht geteilt.

Hatte ich schon erwähnt, dass sich alle genannten Punkte und Geraden mit Zirkel und Lineal konstruieren lassen?

🖖 Живи довго і процвітай