Hallo in die Runde,
mit den Schlägen sind aufeinander folgende Zirkelschläge gemeint...
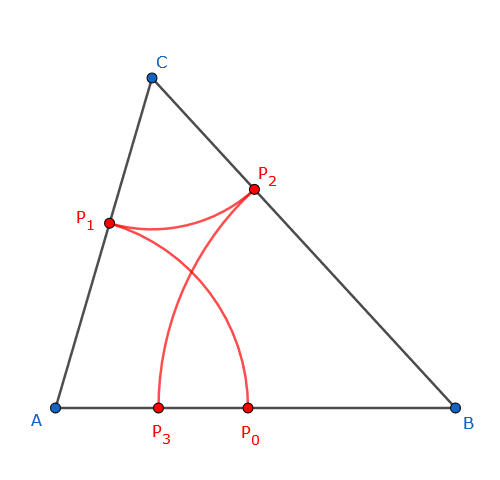
Gegeben ist ein beliebiges Dreieck $$ABC$$ und ein frei gewählter Punkt $$P_0$$ auf der Strecke $$AB$$ (keiner der Endpunkte).
Man schlägt nun mit dem Zirkel einen Kreisbogen um $$A$$ durch $$P_0$$ im Gegenuhrzeigersinn bis zum Schnittpunkt mit $$CA$$, wir nennen ihn $$P_1$$.
Dann schlägt man entsprechend einen Kreisbogen um $$C$$ durch $$P_1$$ bis zum Schnittpunkt mit $$BC$$, genannt $$P_2$$.
Und schließlich einen Kreisbogen um $$B$$ durch $$P_2$$ bis zum Schnittpunkt $$P_3$$ mit $$AB$$.
Anmerkung:
Falls einer der Kreisbögen nicht die angezielte Dreiecksseite trifft,
muss man mit einem geeigneteren Ausgangspunkt $$P_0$$ von vorn anfangen.
In den meisten Fällen, in denen der Dreifach-Schlag gelingt, wird $$P_3$$ vom Ausgangspunkt $$P_0$$ verschieden sein.
| Aufgabe (1): |
|---|
| Welche Bedingung muss $$P_0$$ erfüllen, damit $$P_3$$ mit $$P_0$$ zusammenfällt? |
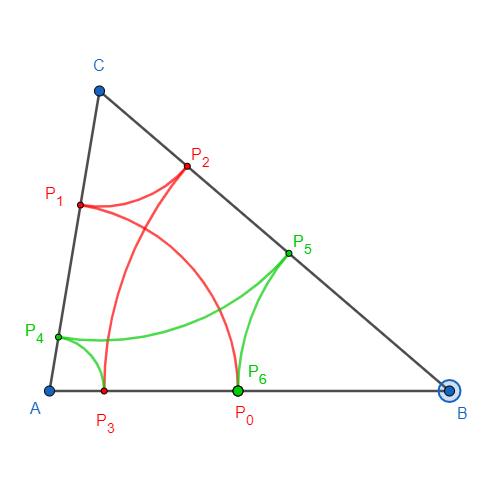
Im Fall, dass die Dreier-Kette sich jedoch nicht schließt, soll die Prozedur mit drei weiteren Zirkelschlägen im gleichen Sinn fortgesetzt werden, so dass man Punkte
$$P_4$$ auf $$CA$$, $$P_5$$ auf $$BC$$ und $$P_6$$ auf $$AB$$ erhält:
| Aufgabe (2): |
|---|
| a) Man stelle eine Vermutung über den Punkt $$P_6$$ an. |
| b) Man beweise diese Vermutung. |
Viele Grüße
ottogal