Hallo in die Runde, ich löse mal auf.
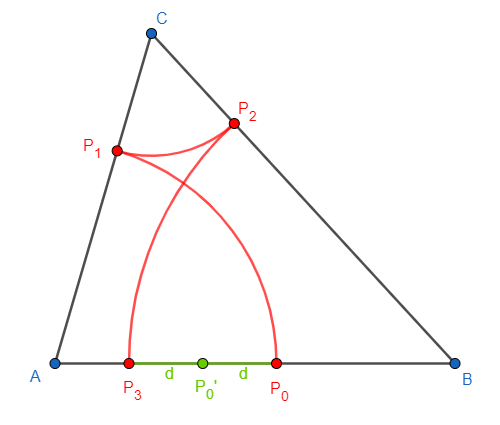
Die Dreiecksseiten seien wie üblich mit a, b, c bezeichnet. Die Radien der Kreisbögen nennen wir der Reihe nach r1 bis r6. Die Lage des Punktes $$P_0$$ legen wir fest durch die variable Streckenlänge $$x = AP_0$$.
Im Folgenden unterstellen wir, dass der gewählte Wert von x alle Kreisbögen erlaubt.
Stes gilt:
r1 = x
r2 = b − r1 = b − x
r3 = a − r2 = a − b + x
r4 = c − r3 = c − a + b − x
r5 = b − r4 = b − c + a − b + x = a − c + x
r6 = a − r5 = a − a + c − x = c − x
Lösung von Aufgabe (1):
Die Bedingung für $$P_3=P_0$$ lautet r3 = c − x, also
a − b + x = c − x
2x = c − a + b
Mit u für den Umfang des Dreiecks, u = a + b + c, und s = u/2 folgt
2x = u − 2a
x = s − a
In diesem Fall gilt also r1 = s − a,
und entsprechend auch r2 = s − c und r3 = s − b;
natürlich ist r1 + r2 + r3 = s.
Den gefundenen speziellen Wert für x nennen wir im Folgenden a', den speziellen Punkt $$P_0'$$.
Bemerkung:
Ist der Radius r1 größer als a', etwa r1 = a' + d, dann wird r2 um d kleiner und folglich r3 um den gleichen Wert d größer.
Die Punkte $$P_0$$ und $$P_3$$ liegen dann also um 2d voneinander entfernt,
und der Mittelpunkt der Strecke $$P_0P_3$$ ist stets $$P_0'$$:
Man kann das gut in der Geogebra-Zeichnung verfolgen, indem man den Punkt $$P_0$$ verschiebt.
Lösung von Aufgabe (2):
Oben erhielten wir r6 = c − x.
Daraus folgt sofort $$AP_6 = AB − r6 = c − c + x = x = AP_0$$.
Das ist der Beweis für die Vermutung, dass $$P_0$$ und $$P_6$$ stets zusammenfallen,
die Sechserkette sich also immer schließt, unabhängig von der Wahl von $$P_0$$.
Zur Konstruktion von $$P_0$$:
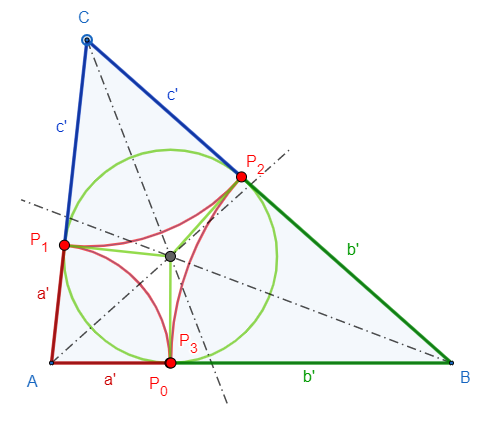
Wenn einem das Bild eines Dreiecks mit Inkreis vor's (vllt. innere) Auge kommt, erkennt man, dass $$P_0$$ der Berührpunkt von AB mit dem Inkreis sein muss:
Die Tangentenabschnitte von einer Ecke zu den benachbarten beiden Berührpunkten sind ja jeweils gleich lang:
$$AP_0=AP_1=a'$$, $$CP_1=CP_2=c'$$, $$BP_2=BP_3=b'$$.
Alle 6 addieren sich zum Umfang:
u = 2a' + 2b' + 2c', also s = a' + b' + c'.
Es folgt a' = s − (b' + c') = s − a, wie oben.
Somit ist $$AP_0'=a'$$, und man erhält $$P_0'$$ als Fußpunkt des Lotes vom Inkreismittelpunkt auf AB.
Anderer Weg:
Im Fall, dass drei Kreisbögen mit $$P_3 \neq P_0$$ vorliegen, konstruiert man den Mittelpunkt $$M$$ der Strecke $$P_3P_0$$.
Nach der Bemerkung oben hat $$AM$$ dann die gesuchte Länge a', es ist $$M=P_0'$$.
Noch ein anderer Weg:
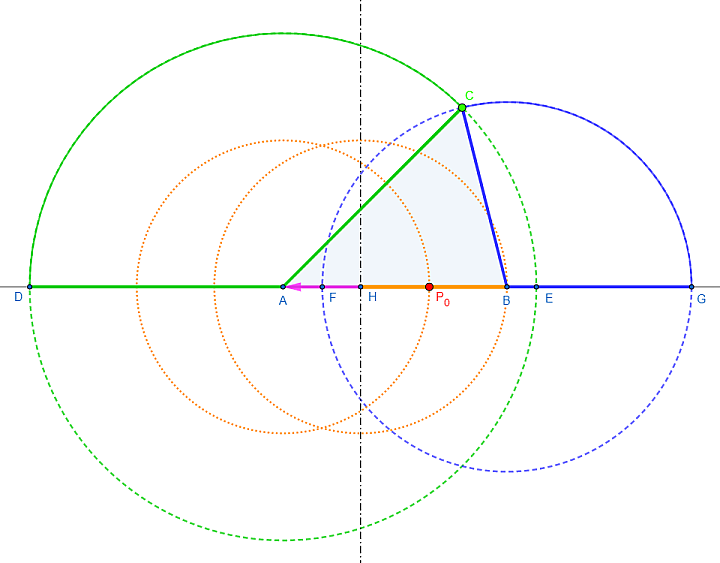
Man konstruiert eine Strecke der Länge a' = s − a.
- Abtragen der Streckenlänge AC von A aus nach links auf die Gerade AB ergibt Punkt D.
- Abtragen der Streckenlänge BC von B aus nach rechts auf die Gerade AB ergibt Punkt G.
- DG hat nun die Länge des Dreiecksumfangs $$u$$.
- Konstruktion der Mittelsenkrechten von DG erzeugt ihren Mittelpunkt H. Folglich hat HG die Länge u/2 = s.
- Wegen HB = HG − BG = s − a = a' ist HB eine Strecke der gesuchten Länge.
- Abtragen dieser Streckenlänge von A aus nach rechts auf AB liefert $$P_0'$$.
Viele Grüße
ottogal