Mathematik - Schlag auf Schlag --- Nachschlag

[ottogal]

Die Schlägerei geht weiter!

(Es sei denn, ihr gebt euch geschlagen – oder schlagt euch in die Büsche...
Mit dem Bisherigen als Vorübung sollte es aber nicht schwer sein.)

Statt mit Dreiecken schlagen wir uns mit Vierecken herum. Die sollen auf jeden Fall konvex sein, d.h. keine einspringende Ecke haben.

Die Seiten benennen wir so: AB = a, BC = b, CD = c, DA = d.

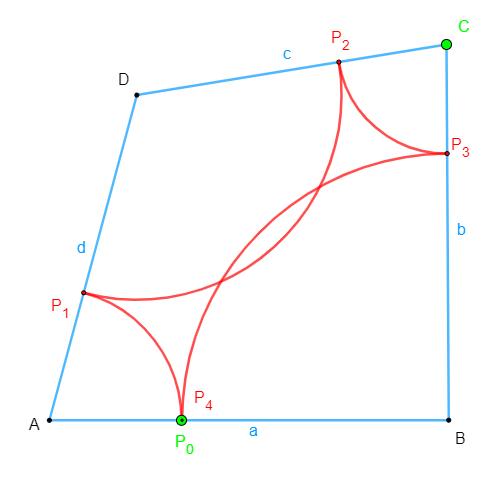
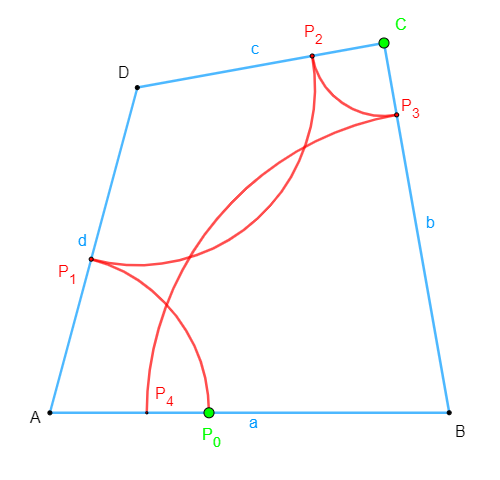
$$P_0$$ sei wieder ein beliebig wählbarer Punkt auf AB, und wir erzeugen (entsprechend wie bei der Dreiecksaufgabe) durch zusammenhängende Kreisbögen um die Ecken A, D, C, B der Reihe nach die Punkte $$P_1$$ auf DA, $$P_2$$ auf CD, $$P_3$$ auf BC und $$P_4$$ auf AB.

Wir unterstellen wieder, dass alle 4 Bögen geschlagen werden können.

Es kommt nun vor, dass die Viererkette sich schließt (also $$P_4$$ mit $$P_0$$ zusammenfällt), oder eben nicht:

Aufgabe (3):
a) Angenommen, bei einem vorliegenden Viereck und gegebenem Startpunkt $$P_0$$ schließt sich die Viererkette. Man zeige: Sie schließt sich dann auch, wenn man einen anderen Startpunkt $$P_0$$ auf AB wählt.
b) Angenommen, bei einem vorliegenden Viereck und gegebenem Startpunkt $$P_0$$ schließt sich die Viererkette nicht. Man zeige: Sie schließt sich dann auch nicht, wenn man einen anderen Startpunkt $$P_0$$ auf AB wählt.

Aufgabe (4):
Welche geometrische Eigenschaft muss ein Viereck haben, damit sich jede Viererkette schließt?

---

Viele Grüße!
ottogal