Hallo in die Runde,
außer @Tabellenkalk hat sich zum "Nachschlag" niemand mehr geäußert - ich löse daher mal auf.
Lösung von Aufgabe (3):
a)
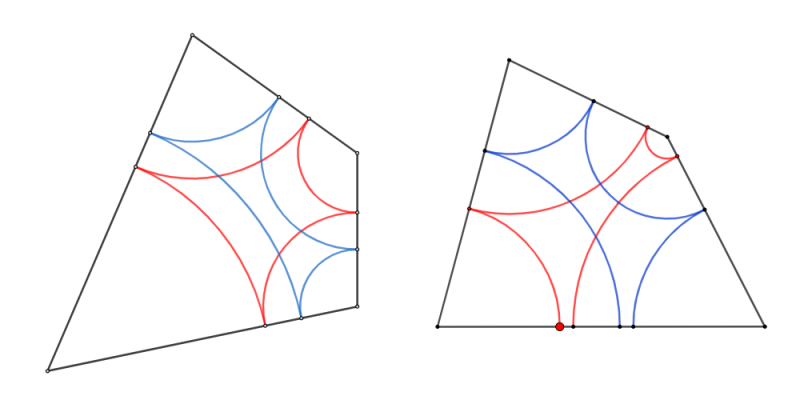
Für die Radien der Kreisbögen gilt hier:
r1 = x
r2 = d - r1 = d - x
r3 = c - r2 = c - d + x
r4 = b - r3 = b - c + d - x
Die Bedingung für $$P_4=P_0$$ lautet r4 = a - r1 = a - x,
also b - c + d - x = a - x
und damit b + d = a + c.
Hier fällt x heraus - die Bedingung ist also nur eine an die Seiten des Vierecks:
Die Längen gegenüberliegender Seiten haben jeweils die gleiche Summe.
Auf die Wahl von $$P_0$$ kommt es nicht an.
b)
Gäbe es eine andere Wahl von $$P_0$$, bei der sich die Kette doch schließt,
würde sie das wegen der Aussage a) auch mit dem Punkt $$P_0$$ tun müssen, im Widerspruch zur Voraussetzung.
Ein anderer Weg:
Die Strecke $$P_0P_4$$ hat die Länge |r1 + r4 - a|, nach obigem also
|x + (b - c + d - x) - a| = |b - c + d - a|, unabhängig von x.
(Man sieht auch hier, dass $$P_4=P_0$$ gleichbedeutend ist mit b + d = a + c.)
Lösung von Aufgabe (4):
Bei der "Schlägerei" im Dreieck spielte der Inkreis eine Rolle. Daher liegt die Vermutung nahe, dass bei einem Viereck, das einen Inkreis besitzt, sich die Viererkette schließt, andernfalls nicht. (Solche Vierecke heißen Tangentenvierecke, weil ihre Seiten den Inkreis berühren.)
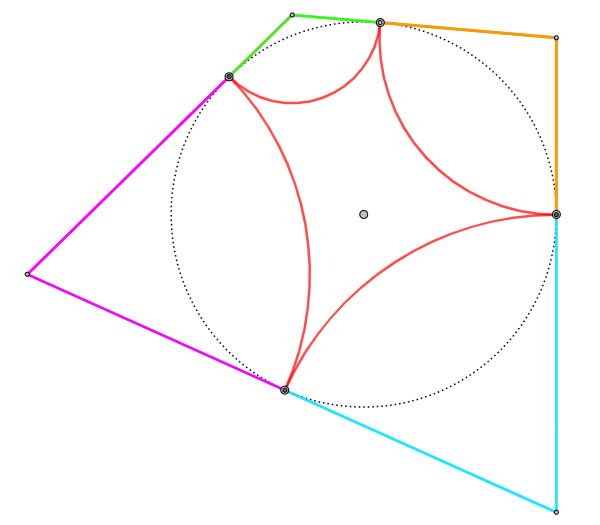
Im ersten Fall sieht man sofort: Wählt man für $$P_0$$ bis $$P_3$$ die Berührpunkte des Inkreises mit den Seiten, erhält man an einer Ecke jeweils gleichlange Tangentenabschnitte bis zum Berührpunkt. Es gibt vier (im allgemeinen verschieden lange) Abschnitte, die jeweils zweimal vorkommen.
Zwei Gegenseiten setzen sich jeweils aus diesen 4 (verschieden gefärbten) Abschnitten zusammen.
Somit bestätigt sich die Bedingung für das Schließen der Viererkette: b + d = a + c.
Diese Gleichheit der Summen der Gegenseiten ist die bekannte Kennzeichnung für ein Tangentenviereck.
Aufgabe (3) a) hat ergeben, dass (anders als bei den Dreiecken) der Anfangspunkt $$P_0$$ nicht unbedingt der Berührpunkt von AB mit dem Inkreis sein muss: Der Wert von x spielt keine Rolle.
In einem Tangentenviereck schließt sich die Viererkette also immer, egal bei welchem Startpunkt $$P_0$$ (auf irgend einer der Seiten!) man anfängt.
Viele Grüße
ottogal